Fig. 1, One person, one perception ...
Ever since I became involved in our community (not to show my age, but this was in the 1970's) I've observed that countless people have noted that they believe they pass most of the time as an individual, but have considerable difficulty when in groups.
It's been my observation that the magic number is three, meaning that any group of more than three will be consistently unable to pass in a general public setting, even though the individuals themselves are indeed quite passable.
In this article, we will attempt to explore why this is indeed the case, and to perhaps quantify what is actually happening.
It has been said that passing is 90% attitude. I tend to agree. Attitude here means not only poise and confidence, but a desire to conform to what is expected and customary. This includes a desire to dress according to the time, place, and circumstance of the activity at hand, and a desire to dress to blend in, not to stand out. I would say that this attitude also includes a desire to not attract attention to one's self. This implies a desire to dress and act in a manner typical of one's age, height, weight, body type, and fitness level.
When I refer to passing and a percentage, for example, "Passes 85%", I'm referring to the fact that such a person will be nonobvious to approximately 85% of the general public observers. It's been my observation that just about anybody, regardless of size or build, can, as an individual, pass to the degree of being nonobvious to at least 75% of the general public.
To reach this value, the person must not only have mastered the technique of underpinning, makeup, outfit selection, etc., but must genuinely want to be perceived by the public as a typical member of the chosen gender. The desire to blend in, not to stand out, must be present. The attitude and confidence must be developed over at least several hours of mainstream public exposure.
For the rest of this discussion, we will use this 80%-passable person as the model for the typical person who is included in our groups.
Our typical person can therefore walk into the average public setting, away from others in the community, and not attract the attention of the vast majority of naive observers.
Intuitively, you would think that if two 80% passable people would appear in public, the probability of the group passing would be .8 * .8 or .64, which would still be passable to the majority of observers.
It's been reported over and over that while one person can usually get away with appearing in mainstream public, two will start to attract stares and double-takes, three will attract much more attention, and four or more will be blatantly obvious.
Let's examine why this phenomenon of significantly diminishing returns occurs.
From the perspective of any one observer, the following is assumed to be true:

Fig. 1, One person, one perception ...
With two people, however, there is a total of three perceptions an observer has of the individual and of the group. There is a perception of each individual, and another of the group as a whole, making a total of three perceptions. Assuming the individuals are both 80% passable, the probability of the group passing is .8 * .8 * .8, or .512, just a bit over 50%.
Fig. 2, Two people, three perceptions ...
In a group of three or more, the number of perceptions becomes more complex. For a group of three, we would have three perceptions, one for each individual, three more, one for each group of two within the group of three, and one additional for the group as a whole, for a total of 7 perceptions an observing individual would have. Again, assuming 80% passabilty for all within the group, the probability of the group passing would be .8 ** 7 or 20.9%.
Fig. 3, Three people, seven perceptions ...
We find that as the group size increases, the number of perceptions a casual observer can have increases drastically. For any group size N, the number of perceptions can be expressed by the formula: perceptions = 2 ** N - 1 If we assume all group members are 80% passable, the probability of a group of N individuals can be expressed by: passability = .8 ** (2 ** N - 1)
| Number in group N |
Number of perceptions 2 ** N - 1 |
Passing probability .8 ** (2 ** N - 1) |
|---|---|---|
| 1 | 1 | .8 |
| 2 | 3 | .51 |
| 3 | 7 | .21 |
| 4 | 15 | .035 |
| 5 | 31 | .001 |
The table above illustrates the number of perceptions and the probability of passing for groups of 1 to 5 individuals. Notice that as the group size increases beyond three, the probability of passing approaches zero for the group as a whole, even though the individuals, when considered and observed alone, would be perfectly passable to the naive members of the general public.
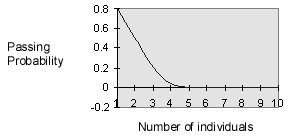
Fig. 4, Passing probability as a function of number of individuals
The above graph shows that, when considering people of 80% passability, the probability of the group passing is for all practical purposes zero for groups greater than three individuals.
Also note that even a group of two or three will have a significantly less probability of passing than any individual making up those groups.
In the real world, a group of equally 80% passable individuals seldom will exist. Yes, if we wanted to do some detailed testing of each individual, and apply some very messy algebra, we could indeed apply these methods to estimate the probability of passability of real world groups.
Lacking the desire to research this phenomenon to that depth, it's fair to assume the following regarding groups in real life in everyday public:
If we apply these methods to the ideal, even if we consider people who are so passable as to be undetectable in the general public, this phenomenon does still take effect. When we consider individuals who are 95% passable, yes, the number in the group can be greater before the passing probability drops into the single digits, a group of 6 or more has essentially zero probability of passing in a naive public situation.
| Number in group N |
Number of perceptions 2 ** N - 1 |
Passing probability .95 ** (2 ** N - 1) |
|---|---|---|
| 1 | 1 | .95 |
| 2 | 3 | .86 |
| 3 | 7 | .69 |
| 4 | 15 | .46 |
| 5 | 31 | .20 |
| 6 | 63 | .039 |
The above table represents close to what is the best that can be expected in the real world. 95% passable individuals are quite exceptional, and is is indeed a rare occasion when a group of members of the community consists of those of this passability. This table is meant to illustrate that the phenomenon still applies even under circumstances that would be considered close to ideal.